Introduction to OCaml, part 4: higher order functions, parametric polymorphism and algebraic data types
Last update:
Tags:
Note: new chapters are not posted in the blog anymore! Improved and expanded versions of these posts and new chapters can be found on the OCaml Book project website.
Higher order functions and parametric polymorphism
Parametric polymorphism
So far we have only worked with functions that take value of a single type known beforehand.
However, we have already seen functions whose types were left without explanation, such as
let hello _ = print_endline "hello world" that we used to demonstrate the wildcard pattern.
What is its type? If you enter it into the REPL, you will see that it's 'a -> unit.
What does the mysterious 'a mean? Simply put, it's a placeholder for any type.
Essentially, a variable for types —a type variable.
It is easy to see that this function indeed works with arguments of any type and behaves the same:
let hello _ = print_endline "hello world"
let () = hello ()
let () = hello 1
let () = hello false
This program will compile just fine and print hello world three times.
The wildcard pattern just discards the value. Will the behaviour or type of this function
change if we write it let hello x = print_endline "hello world" instead? If you experiment
with it, you will see that it doesn’t. It seems logical: since the argument is still not used
in the function body in any way, its type shouldn’t matter, and in the OCaml’s type system,
it indeed doesn’t.
This is known as parametric polymorphism.
There are two kinds of polymorphism in programming languages. The first kind, which is more
popular, is called ad hoc polymorphism, and is also known as function/method/operator overloading.
It is the ability to use two or more functions with the same name but different type and behaviour
in the same program, for example, make + behave like addition for numbers but concatenation
for strings. The majority of structured and object oriented languages implement it.
Parametric polymorphism is ability to use the same function for values of any type. It is relatively more rare, but is gaining acceptance, for example in Scala and Swift, even though it’s often not mentioned by name.
Some languages, such as Ada, Java, or C++ clearly recognize the issue and provide a mechanism of generics or templates that can be instantiated for different types. If you are familiar with them you can think of polymorphic functions as generics that need not be instantiated.
Since OCaml doesn’t support ad hoc polymorphism (it would require sacrificing the ability to write statically typed programs without any type annotations), hereafter the word polymorphism refers to parametric polymorphism.
Just like generics in Ada or Java, parametric polymorphism is often used to implement collections that work with items of any type, but prevent attempts to use items of different types in the same collection which would ruin type safety. We will learn about polymorphic collections a bit later, after we learn about their building blocks — algebraic data types.
A note on notation
A lot of time on the blackboard and in publications, people use small greek letters for type variables, such as
α, β etc. where actual source code uses 'a, 'b and so on.
You can also see types of polymorphic written with universal quantifier: ∀ α . α → α.
It is to emphasize that the type variable can be substituted with any type, that is, for any type α function f
can be specialized to it, i.e. become int -> int, or string -> string, or something else.
Higher order functions and combinators
The function we used for demonstration is the simplest example of parametric polymorphism, but it’s quite useless since it doesn’t do anything with its argument, so let’s move on to its more interesting application — implementing type safe higher order functions.
You may already be familiar with higher order functions from other languages, for example
Python or Ruby. They both, and many other, provide a map function that takes a function
and some kind of ordered collection and applies it to its every element. Since they are
dynamically typed, if the type of that function is wrong, it will cause runtime errors.
In a dynamically typed language all is required to support higher order functions is support
for first class functions (i.e. functions as values).
OCaml is statically typed, higher order functions need to be polymorphic to be able to apply functions of different types to different arguments.
Since we are not ready for polymorphic collections yet, we’ll consider simpler but useful examples that require nothing but functions — combinators. A combinator, strictly speaking, is an expression that has no free variables. Loosely, that term is often used for any functions that help you make new functions from existing one.
Let’s examine two combinators from the standard library that can make your life easier: @@ and |>.
The @@ operator (and remember, operators are functions) takes a function and some other value and applies a function to that value.
Its practical use is to reduce the number of parentheses you need in your expressions. Compare these equivalent expressions:
let () = print_endline (string_of_int 5)
let () = print_endline @@ string_of_int 5
If it was not in the standard library, it could be trivially defined as:
let (@@) f x = f x
Its type is ('a -> 'b) -> 'a -> 'b. It means that it takes a function of type 'a -> 'b (that is, from any type
to any other type) and applies it to a value of type 'a. It guarantees that if the type of the value does not
match the return type of the function, the program will fail to type check. While the type variable 'a by itself
can stand for any type, if it appears on both sides of an arrow, the type is stands for must be the same on both
sides too.
Here is an example of an incorrect program:
let () = print_endline @@ 5
Another useful combinator is the reverse application combinator written |>. It is conceptually similar to the
application combinator @@, but it differs in that it has a value on the left hand side and a function on the
right hand side. It can be defined as:
let (|>) x f = f x
Its type is 'a -> ('a -> 'b) -> 'b. This is useful if you want to take a value and send it down a computation pipeline, for example:
let () = 5 |> string_of_int |> print_endline
The pipeline can be of any length, and can help you avoid a lot of extra parentheses in nested expressions, and make them much easier to edit.
Now let’s make our own combinator that the standard library doesn’t provide: function composition. It will take two functions and a value and apply them both to it:
let (+*) f g x = g (f x)
Its type is ('a -> 'b) -> ('b -> 'c) -> 'a -> 'c. Since the value is its last argument, we can produce a new
function using it without mentioning any arguments at all, thanks to partial application:
let (+*) f g x = f (g x)
let print_int = print_endline +* string_of_int
let () = print_int 5
The type of the +* function we created is ('a -> 'b) -> ('c -> 'a) -> 'c -> 'b. The types of both
functions it takes are enclosed in parentheses because arrows associate to the right, and we have to
group them explicitly to avoid confusion with a function of five arguments.
Combining functions without explicitly mentioning arguments, like we did in let print_int = print_endline +* string_of_int
is referred to as point-free style. The word “point” here refers not to the dot character, but
to the function argument, generalizing its use for mathematical functions that take point on a line or a plane.
Using it excessively can make programs hard to follow, so use your judgement.
Algebraic data types and pattern matching
So far we’ve only seen typed that can encode single values, such as integers, strings, or functions. Practical programming, however, is nearly impossible without composite types. Tuples, lists, trees, and other datastructures are staples of software development.
The most common building blocks of composite types in OCaml are so called algebraic data types (ADTs). While OCaml has records, objects, and arrays too, the most common built-in types are ADTs.
Algebaric types are closely connected with pattern matching and explaining them has something of a chicken and egg problem: it is impossible to explain pattern matching without explaining algebraic types, but algebraic types make little sense until you know how to use them in pattern matching. We will try to break the circle by learning how to define them by example, and then learning how to actually use them.
Product types
Product types are also known as tuples. They get their name from their relation to the cartesian product of sets. A cartesian product of two sets A and B is a set of pairs of all items of A and B. For example, a plane is a product of a line with itself.
This is how we could define a type of points on a plane:
type point = float * float
Note that while you can define a named product type, they are usually left unnamed, and if you call a float * float
type point, the OCaml compiler will not start referring to any value of type float * float as point.
The * operator is a type constructor that creates a new product type from two other types, in this case
a tuple of two floats. You can create tuples of more than two items in the same fashion:
type point3d = float * float * float
This is just the type though, and naming product types is not a standard practice. Values of product types use comma as an item separator, like in many other languages. Note that parentheses around tuples are optional and required only when leaving them out will cause ambiguity.
let zero = 0.0, 0.0
Sum types
Sum types generalize what is often known as enum, union, or variant record. They are also rather harder to explain than product types because they have no direct equivalent in most languages.
Mathemarically, a sum type is a disjoint union: a union of sets where every element is attached to a tag indicating which set it came from.
The simplest kind of a sum type is used to model finite sets. This is equivalent to enums in C-like languages.
type chess_piece = Pawn | Knight | Bishop | Rook | Queen | King
This is the simplest use case however, and their greatest expressive power comes from the ability to attach values to sum type members. For example, suppose we are writing a geometry program and we need a type for shapes. A circle can be defined by its radius, a square by its side length, and a triangle can be defined by lengths of its sides. So our type may look like this:
type shape = Circle of float | Square of float | Triangle of (float * float * float)
Sum types can also be polymorphic. For example, there is a type in OCaml standard library that is meant for functions that can produce some value or no value at all, it is called option. For example, searching for something in a database can produce a list of results, or not find anything, and it is nice to be able to encode the latter case explicitly. The option type can be defined as follows:
type 'a option = Some of 'a | None
There is also a type meant for functions that can explicitly signal error conditions:
type ('a, 'b) result = Ok of 'a | Error of 'b
As you can see, polymorphic types need to have one or more type variables on their left hand side.
Terminology and syntax
You should remember that user-defined data constructors must always start with a capital letter.
The anatomy of a sum type definition is shown in the following picture:
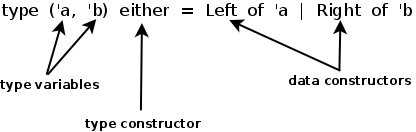
The name of the type is referred to as type constructor, because it can used to create new monomorphic types
with different type variables, such as int option or string option, or (int * string) result and
(float * unit) result.
Names of sum type members are called data constructors, since they can construct new values from existing ones,
such as Some 3 or Error "Not found".
The truth about unit and boolean values
While there is special syntax for the unit value () and boolean constants true and false,
internally, they are just sum types.
If special syntax didn’t exist for them, they could be defined as:
type unit = Unit
type bool = True | False
Pattern matching
Now it’s time to learn about
We have already seen some basic use of patterns, and learnt that the left hand side of let-bindings,
including function definitions, is a pattern.
Here is what we know is a valid pattern:
- A variable name
- A constant
-
The wildcard (
_).
Now we can add that a tuple, any defined data constructor, and any combination thereof is also a valid pattern.
Patterns in let-expressions
Let’s see how we can use tuple and data constructor patterns in let-bindings.
Some languages have special constructs for multiple assignment.
In OCaml, you can do the same by using a tuple pattern, so no special construct is needed.
let a, b = 1, 2 in
Printf.printf "%d %d\n" a b
If you have a function that returns a tuple, and you only want one item of that tuple, you can combine the tuple pattern with the wildcard pattern to discard the unwanted part:
let f x y = x, x + y
let _, x = f 3 2
let y, _ = f 3 2
let () = Printf.printf "%d %d\n" x y
The relationship of let-bindings with sum types is more complicated. While they can technically be used on the left hand
side of a let-expression, if your type has more than one data constructor, it will result in unhandled cases,
which will result in compile time warnings and runtime errors.
Consider this program:
let x = None
let (Some y) = x
let () = Printf.printf "%d\n" y
If you compile and run it, or paste into the REPL, you will get this warning at the compilation stage:
Warning 8: this pattern-matching is not exhaustive.
Here is an example of a case that is not matched:
None
And at the execution stage it will fail with Match_failure exception. While you could catch that exception
(we will learn about exceptions later), it would be a very unidiomatic thing to do. Types with more than one
data constructor should be handled by proper cases analysis with match expressions that are covered by the
next section.
The unit type is an exception to this rule, since it has only one possible value and thus immune to match
failures. That is why it can safely be used in let-expressions when you want to enforce that the expression
on the right hand side evaluates to unit.
Match expressions
In OCaml, match expressions play a role similar to case or switch in many other languages, but
due to pattern matching support, have more expressive power.
Their simplest use can be demonstrated on primitive types, such as int. Constants of any type are valid patterns,
and we can match on them.
Let’s compare functions that
determine is given number is zero, written with a conditional expression and pattern matching:
(* With a conditional *)
let is_zero n = if n = 0 then true else false
(* With a match expression *)
let is_zero' n = match n with 0 -> true | _ -> false
In multi-line match expressions, some people like to add a | character before the first case as well, for
visual uniformity:
let is_zero n =
match n with
| 0 -> true
| _ -> false
A function determines if given character is a whitespace character or not can be a more interesting example:
let is_whitespace c =
match c with
' ' -> true
| '\t' -> true
| '\n' -> true
| '\r' -> true
_ -> false
You can see that it’s rather repetitive. To avoid repetition, OCaml allows conflating cases:
let is_whitespace c =
match c with
' ' | '\t' | '\n' | '\r' -> true
| _ -> false
So far this is equivalent to switch statements in C-like languages, so let’s move on to
more interesting patterns that allow us to destructure complex values.
To demonstrate using tuple patterns inside match expressions, we will reimplement the logical AND function.
Logical AND is only true when its both arguments are true, otherwise it’s false. With a match expression
and a tuple pattern we can express it consicely:
let (&&) x y =
match (x, y) with
| true, true -> true
| _, _ -> false
We could use nested matches, but that would be unwieldy. Instead, in the match expression,
we join both arguments into a tuple so that we can match on them both at the same time in our
cases, and this way we need only two cases.
Now let’s see how we can combine data constructors of sum types and tuples in pattern matching. Remember the type for geometric shapes that we introduced earlier. This is how we can write a function for calculating the area of different shapes:
type shape = Circle of float | Square of float | Triangle of (float * float * float)
let area s =
match s with
| Circle r -> Float.pi *. (r ** 2.0)
| Square s -> s ** 2.0
| Triangle (s1, s2, s3) ->
let s = (s1 +. s2 +. s3) /. 2.0 in
sqrt @@ s *. (s -. a) *. (s -. b) *. (s -. c)
let () = Printf.printf "%f\n" @@ area (Triangle (3.0, 4.0, 5.0))
Nested match expressions
In the logical AND function, we managed to get away with a single match expression,
but there are cases when nesting them is unavoidable. The issue you should be aware of is that,
since indentation in OCaml is not significant, nested matches need explicit delimeters.
Like any other expressions, you can wrap them in parentheses, but there is also syntactic sugar
in form of begin and end keywords. They are syntactically equivalent to parentheses, to the point
that the unit value can be written as begin end, as in print_newline begin end, though using them
in this role is obviously bad for readability. But for grouping expressions, they can provide
a readability improvement.
Let’s rewrite our logical AND function in an overly verbose way for demonstration.
let (&&) x y =
match x with
| true ->
begin
match y with
| true -> true
| false -> false
end
| false -> false
If you forget to group match expressions properly, they will be treated as one long match, which
may cause type errors, or, worse, break your program logic.
A note on exhaustiveness check
As we have already seen, the OCaml compiler performs match exhaustiveness checks and warns you if it finds
a case that is not handled. The checking mechanism is consistent (free of false negatives), that is, it will never fail to spot a
genuine unhandled case. However, it is not complete (not free of false positives), and sometimes will
issue warnings when matching is actually exhaustive. This happens especially often if you use nested match expressions.
The compiler warnings must be taken seriously. Only if you can prove that your matching is indeed exhaustive, then you can safely ignore them.
Exercises
Write a function twice that takes a function f and a value x and applies f to x twice.
Try to predict its type before you check it with the REPL or another tool.
Simple: write a function with type 'a -> unit.
Somewhat harder: write a function with type ('a -> 'b) -> ('b -> 'a) -> 'a -> 'b.
Define a sum type that models a card deck.
Using a match expression, write a function is_vowel : char -> char that checks if given
character is a vowel.
Write a function with deliberately non-exsaustive pattern matching and cause it to fail with Match_failure exception.
Write a logical XOR function using a match expression and no more than three cases.
Extend the shape type and the area function with one or more new shapes of your choice.
Continue to part 5.