Introduction to OCaml
Last update:
Tags:
Preface
Note: new chapters are not posted in the blog anymore! Improved and expanded versions of these posts and new chapters can be found on the OCaml Book project website.
This post series started as a response to requests from some friends curious about OCaml. There are quite a few nice books already, but I realized that if I just recommend them any one of those books, it still will leave me with quite a few things to explain in depth, or force me to recommend another just to learn about that part. So I thought I may as well write something that hopefully will allow a person who already knows how to program in some other language get started with writing OCaml programs and continue learning on their own and find their own sources.
I decided to follow these principles:
- Do not make it REPL-centric. Real life programs are not developed in the REPL. Include examples of complete programs.
- Do not introduce any concept before enough background is given to explain it without unjustified simplifications. Incomplete truth is better than a lie.
- Provide motivating examples and explain pathological cases.
- Do not mention foxes or chunky bacon.
Is OCaml hard to learn? Yes and no. It’s easy to learn because it’s not a “puzzle language” — its rules are generally hard and fast, and its syntax and semantics are predictable. However, it’s also harder to learn than most popular languages because it uses ideas that are only starting to gain wide acceptance. It is not unlike the difference between the assembly languages and first structured programming languages.
Why would one want to use it? Here are some points:
- Very fast compiler. The reference implementation of OCaml can bootstrap itself within minutes.
- Static typing without a need to write any type annotations by hand.
- The type system is expressive enough to find some classes of logic errors, not just misplaced variables.
Its traditional domain is compiler writing and automated theorem proving systems. For example, Coq proof assistant, that was used to create the first C compiler where all optimizations are mathematically proven correct, is written in it. The Rust compiler was written in OCaml until it was able to compile itself.
More recently, it also started to be used by financial companies such as Jane Street and Lexifi for their automated trading software, and tools for cross-compiling it to JavaScript allowed using it for web applications. For example, the web version of Facebook Messenger was largely rewritten in OCaml with alternative syntax.
A bit of history
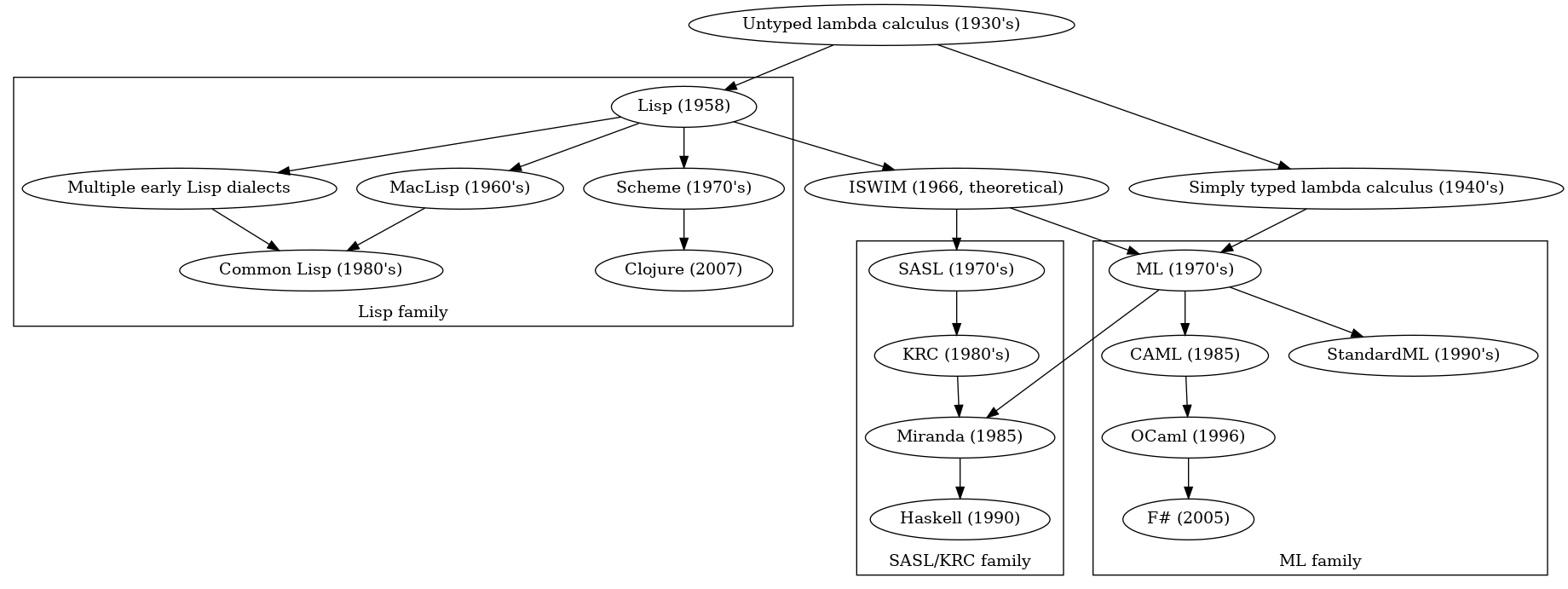
OCaml itself is not new. It was first released as a distinct language in 1996, and even has one direct descendant — F#, that even includes syntax compatibility mode. However, the history of the ML language family is even longer and goes back to the 70’s, and the theory that made those languages possible is even older yet, dating back to the 30’s — it is called the lambda calculus.
Here is a brief and simplified story.
In the 30’s, mathematicians took intense interest in the concept of computability. They could be called computer scientists even though general purpose computers didn’t exist yet, and they were creating the foundations for their development. The main questions of the computability theory are what problems can be solved by algorithms, and how to reason about algorithms, for example, how and when can we find out if an algorithm always terminates. It required computation models, and multiple models were developed independently.
Alan Turing developed the well known abstract machine that is now called Turing machine — an infinite length tape and a head that can read and write symbols to the tape cells. Independently, Alonzo Church and Haskell Curry found that it is possible to model arbitrary computations using nothing but functions — that was the lambda calculus. Then it was discovered that the two models are equally powerful.
In the 40’s, the lambda calculus was extended with a concept of types. Types were invented even before the lambda calculus, and long before computers, as an alternative to the set theory that would be free of its paradoxes (Bertrand Russel, who discovered a famous paradox, worked on type theory extensively). However, it took a while longer for the typed lambda calculi to take root in computers languages, and the first languages based on it were untyped.
The Turing machine is roughly the model behind imperative languages such as C and Fortran. The first language closely related to the lambda calculus was Lisp developed by John McCarthy in 1958. For a while, all functional languages were untyped (or dynamically typed).
However, in the 1970’s, J. Roger Hindley and Robin Milner independently discovered a type system that allowed to unambiguously infer types of all expressions in a language without any type annotations. Then Milner et al. developed an algorithm for doing it efficiently, and created a programming language called ML (Meta Language) that was statically typed but made type annotations entirely optional, since it could infer all types and detect type errors on its own.
Initially, ML was an embedded language of a theorem proving system, but later took a life of its own, and people (I need to research who did it first) discovered a way to extend it with mutable references and exception handling in a type safe manner at cost of a small restriction. Now it was suitable for general purpose programming.
ML had multiple descendants, most of them research languages not intended for production use. Its type system was also incorporated into the family of programming languages that led to creation of Haskell, though whether Haskell belongs to the ML family or not is debatable.
The original ML went through a process of standardization in the 1990’s and its entire specification was mathematically proven to be consistent by Robert Harper et al., which is a truly outstanding result. However, its specification was not extended since 1997, and it’s rarely used now, even though it remains fairly popular for teaching and a few theorem proving systems still use it. One notable modern project that uses it is Ur/Web, a specialized programming language for web development.
Another ML descendant called CAML remained under active development, and eventually evolved into OCaml we know today. Along with F#, it remains the most common ML in production use now.
The implementation
OCaml is probably unique in that its reference implementation includes all of native code compiler for multiple platforms, a bytecode compiler, and an interactive interpreter. Standalone program normally use the native code compiler, while the bytecode is only used on platforms not supported by it, With third-party tools, it can also be cross-compiled to JavaScript, and the tools are powerful enough to allow running OCaml itself in the web browser, you can find a real example of it at try.ocamlpro.com.
The implementation is licensed under GNU LGPL and is available from ocaml.org. On UNIX-like systems, however, the fastest and most convenient way to install it is to use OPAM, the OCaml package manager. Unlike most similar tools such as Python’s pip or Haskell’s cabal, OPAM allows installing the compiler itself, keeping multiple compiler versions on the same machine, and switching between them, in addition to installing OCaml libraries.
OPAM for Windows, however, is still under development, so I will not cover it yet.
When you have OPAM installed, use the opam switch command to install the compiler. At the time of writing, the latest version is 4.07, so the
command will be: opam switch 4.07. When it completes, you may want to run this command to setup the environment varibles without restarting your shell:
eval $(opam config env).
Once you are set, you can verify the installation by executing the three main programs: ocamlc (the bytecode compiler), ocamlopt (the native code compiler),
and ocaml (the interactive interpreter). The first two should exit without any output, the third one starts the interactive top level where you can
enter expressions and have them evaluated — more on that later.
Using the REPL
The interactive interpreter allows you to enter expressions and have them evaluated. One thing you should note is that it uses double semicolon
as an end of input mark, so you should terminate all expression with ;;.
The default REPL is quite minimalist and doesn’t even support command history. You can either alleviate the issue with rlwrap,
or, better, install utop from OPAM (opam install utop). It is an alternative REPL that supports history, completion, and more.
While the examples here tend to be compiler-centric, you should not neglect the REPL. First, it’s the quickest way to find out the type
of any function without even opening the documentation: just type something like print_endline ;; and you’ll see the type.
Second, any valid OCaml program can pasted into the REPL or its file can be loaded into it with #use "somefile.ml";; directive.
It is even possible to run OCaml programs in the same fashion as Python or Ruby scripts with ocaml file.ml.
It is also possible to load compiled libraries into the REPL, but we’ll not discuss that part now.
Starting out: bindings, variables, and expressions
The structure of OCaml programs
An OCaml program, loosely speaking, is a sequence of expressions evaluated from top to bottom. There is no designated main function. There are also no statements in OCaml, everything is an expression, all expressions have values, and all values have types.
This is an absolutely useless but valid OCaml program:
1
You can save it to file, for example one.ml and compile it with ocamlopt -o one ./one.ml. The executable it produces will exit immediately.
What happens there? It’s a program with a single expression, 1, which is a constant of type int. Constants evaluate to themselves, so this
program evaluates 1, which produces no effects, and exits, since it has nothing else to do.
A constant is an example of a pure expression. It produces no side effects such as input/output, and it stays the same no matter how many times it’s evaluated. An expression can also be impure, if they produce side effects, or evaluate to a different value if you evaluate it more than once (like a function for getting current system time, for example).
Constants and types
So, integer literal 1 is a constant of type int. Let’s look at some other kinds of constants we can use:
-
4.0,3.5,1.— floating point literals have typefloat. -
'c','\n'— character literals have typechar. -
"foo","bar\n"— string literals have typestring -
true,false— boolean literals have typebool
This list is not complete, but it’s enough for the start.
Function application and Hello World
Now let’s write a slightly less useless program, the traditional “hello world”.
For this we’ll need to use a function. The standard library function that prints a string with a newline
at the end is print_endline, there’s also print_string function that doesn’t add a line break.
The syntax for function application is very simple: function name followed by its arguments. You need no parentheses or any other special syntax.
This is a Hello World program:
print_endline "hello world"
Now compile it and try it out:
$ ocamlopt -o hello ./hello.ml
$ ./hello
hello world
For the sake of experiment, you can try applying the print_endline function to a non-string constant
and get your first type error:
$ cat hello.ml
print_endline 1
$ ocamlopt -o hello ./hello.ml
File "./test.ml", line 1, characters 14-15:
Error: This expression has type int but an expression was expected of type
string
This is type inference in action: the compiler inferred the type of 1 as int, checked the type of the print_endline
function, and found that it expects a string. How it knows that int is a wrong type to use with print_endline though?
By checking it against the type of that function.
The type of functions and the unit type
In OCaml, like in any functional language, functions themselves are values. If functions are values, they must also have types.
By typing print_endline;; in the REPL you can see that its type is string -> unit.
The arrow signifies that it’s a function from a type named string to another type named unit.
When the compiler encountered the print_endline 1 expression, it knew that the type of 1 is int rather than string,
and from the type of print_endline it knew that its argument must be string, so it was able to detect the type error.
Now let’s examine the “return type” of that function on the right hand side of the arrow.
We are already familiar with string, but the unit is new. What is it and why it’s needed?
As you remember, all expressions have types,
so when print_endline "hello world" is evaluated, the result of evaluation must have some type. A function in OCaml
cannot “return nothing”.
Since many functions are used just for their side effects and don’t produce any useful values, some type must have
been invented just to have them comply with the “all values have types” rule.
The unit type is a type that has only one value, and it was invented specially for this purpose. Its only possible value
is a constant written ().
Whether it was made to look this way to mimic calling functions without arguments in other languages
is debatable, you should just remember that the constant () has type unit.
The unit type is also used for functions that take no useful arguments, but have to take something because in OCaml a function cannot have no arguments either. The “arrow type” must always have both left and right hand sides.
An example of a function with unit -> unit type is print_newline that just prints a line break.
A program that prints a line break thus can be written as:
print_newline ()
Programs with multiple expressions and variables
So far we have only written programs that consist of a single expression. Let’s see how to introduce variables and how to use multiple expressions — in OCaml these concepts are related.
To create a variable, you bind a value to a name. They are variables in mathematical sense, their value generally cannot change, even though the same name can be bound to a different value in a different scope. Variables are also called bindings.
Bindings are created with the let keyword. There are two ways to use let-bindings: one allows you to make a binding accessible
only to one expression that follows it (let <name> = <value> in <expr>), while the other (let <name> = <value>) makes a binding
accessible to all expressions below it. This is not a standard OCaml terminology, but for convenience let’s call them local
and global bindings respectively.
Let’s rewrite the Hello World program with a local binding:
$ cat ./test.ml
let hello = "hello world" in print_endline hello
$ ocamlopt -o test ./test.ml
$ ./test
hello world
We could also use two bindings instead of one to demonstrate that let ... in constructs can be nested:
let hello = "hello " in
let world = "world" in
print_endline (hello ^ world)
The ^ operator here is string concatenation. What happens here? Earlier I said that in the let ... in form,
the binding will only be available to the expression that follows the in keyword, but remember that let-bindings
are themselves expressions, and they can be chained.
Every let-binding opens a new scope.
Here we first create a scope where the name hello is bound to a string constant "hello ", then inside it
we create a scope where the name world is bound to a string constant "world", and in that scope,
evaluate the print_endline (hello ^ world) expression.
Now let’s try global bindings. Before we can try them, we need to learn how to use multiple expressions in our programs. You might have already noticed that we have not used a semicolon or another statement terminator. Simply writing:
print_endline hello
print_endline world
will not work because it will be parsed by the compiler as an attempt to apply the print_endline function to three arguments, of which
the first is a string, the second if a function, and the third is string again; and this will fail because
the type of print_endline is string -> unit. In the example above we avoided the issue by applying
print_endline to another expression in parentheses, but this isn’t always feasible.
How do we make a program with multiple independent expressions parse correctly then?
It’s time to learn a secret of let: its left hand side is not just a name, but a pattern.
Patterns have multiple uses and forms, which we will explore later. For now, you need to know that a name
is a pattern. Another possible pattern is the wildcard pattern written _, which comes in handy when
you need to have an expression evaluated, but don’t want to bind its value to any name.
To create independent top level expressions you may make “fake” bindings with wildcard patterns:
let hello = "hello "
let world = "world"
let _ = print_string hello
let _ = print_endline world
A constant is also a valid pattern. As you remember, the type of print_endline is string -> unit, so it always
evaluates to the () constant. Thus you can also write:
let () = print_string hello
let () = print_endline world
In this case you need to watch that the constant pattern on the left hand side and the expression on the right hand side
have the same type, but when you start using more complex expressions, this can also serve as a useful safeguard against
accidentally using an expression of a non-unit type on the right hand side. While the wildcard pattern accepts values of
any types in the let-binding context, a constant pattern, such as (), will force type checking.
If you know that your expression must have type unit, it’s always better to write let () = rather than let _ =.
Here is an example of an error that is made invisible by the wildcard pattern:
let _ = print_endline
The program incorrect, but syntactically valid because functions are values, and the right hand side of a let-binding can be any value,
including a function.
In this example it’s obvious that the argument is missing, but if print_endline function had more arguments, it would be
easier to forget one. Since the wildcard pattern completely ignores the right hand, the program will compile, but print nothing.
However, if you use the unit pattern, the program will fail to compile because print_endline function is not a value of type unit:
let () = print_endline
Finally, if you have multiple expressions of the unit type, you can chain them using semicolons. In OCaml, the semicolon
is an expression separator rather than a statement terminator, so you will need at least one unit or wildcard binding to use it though:
let helloworld = "hello world"
let () = print_string helloworld; print_newline ()
If you try this with expressions of types other than unit, the compiler will produce a warning. To suppress the warning,
you can apply the ignore function to your expression, as in:
let () = ignore 1; print_endline "hello world"
Finally, you can also use ;; like in the REPL, but it’s a very bad style and should be avoided whenever possible.
Shadowing
As you remember, every new binding opens a new scope. We can illustrate it like this:
(* Scope 0 *)
let hello = "hello " (* Opens scope 1 *)
(* Scope 1 *)
let world = "world" (* Opens scope 2 *)
(* Scope 2, (hello = "hello ", world = "world") *)
let () = print_endline (hello ^ world)
Now let’s stop and think what happens if we make two bindings with the same name.
(* Scope 0 *)
let hello = "hello"
(* Scope 1 *)
let hello = "hi"
(* Scope 2 *)
let () = print_endline hello
If you compile this program and run it, you’ll see that it prints hi. This is because the second binding
redefined the value of hello in the scope 2. This is called shadowing. It is distinct from variable
assignment. The original value of hello did not change, it just becomes inaccessible from the new scope
where it was redefined. Is the original value of hello lost forever? In the example above, yes, it will be
completely inaccessible. In general case, the question is more interesting, but we will lean about it later
when we get to functions and closures.
The case when difference from variable assignment is especially visible is the let ... in bindings.
It is perfectly safe to redefine a binding locally and it will have no effect on the rest of the program.
Consider this program:
(* Scope 0 *)
let hello = "hello "
let hello = hello ^ "world" in
(* Local scope 1 *)
print_endline hello
(* Back to scope 0 *)
let () = print_endline hello
It will print hello world, and then print hello, because our let ... in binding only redefined the hello
variable for the print_endline hello expression.
Arithmetics
Now that we know how to use expressions and bindings and have basic idea of how function types work, we can look at the arithmetics.
As we’ve seen earlier, integer and floating point numbers are distinct types in OCaml. The character type is not a numeric type and cannot be used in arithmetic expressions.
An unusual feature of OCaml is that it also uses different sets of arithmetic functions for integers and floating point numbers. The reason for it is that otherwise the language would require either support for ad hoc polymorphism, which would ruin the decidable type inference without any type annotations; or magical overloading specially for arithmetics. The language designers sacrificed some convenience for consistency.
The integer operators look as usual: +, -, *, /. The floating point operators have a dot at the end:
+., -., *, /..
let a = 4 + 2 (* good *)
let b = 4.0 *. 3.5 (* good *)
let c = (float 4) +. 2. (* good, integer is converted to float *)
let d = 4.0 + 2.0 (* bad, using an integer addition with floats *)
let e = 4 +. 2 (* bad using a floating point addition with integers *)
let f = 4.0 + 2 (* bad, mixing floats with integers *)
Now let’s write a program that takes temperature in Celsius from the standard input and converts it to Kelvin.
let celsius = read_float ()
let kelvin = celsius +. 273.15
let () = print_float kelvin; print_newline ()
Let’s verify that it works:
$ ocamlopt -o kelvin ./kelvin.ml
$ ./kelvin
20
293.15
Exercises
Write a program that takes an integer from the standard input and prints its square. Use read_int function
for reading and print_int for writing.
Write a program that takes a floating point number representing temperature in Celsius from the standard input and converts it to Fahrenheit.
Continue to the part 2.